In nearly each new neural community you’re employed on, you´ll want a dataset for coaching. In sequential datasets, these the place the order of the info is vital (as in RNN and LSTM), you usually discover a column with a timestamp, a date, an hour, together with the goal knowledge columns that might be used for coaching.
Often, you employ this time knowledge to order the info sequentially, then you definately extract the info from the goal column or columns for processing with out additional consideration of the time column.
However earlier than swiftly discarding this time column, think about whether or not this time knowledge holds relevance to the goal knowledge. Decide if it contributes worth or significance to the dataset, aiding the neural community in comprehending variations throughout the sequence and subsequently enhancing predictions.
To make this evaluation, ponder your dataset and study if there exists a possible correlation between the goal knowledge and the time knowledge.
As an example, climate metrics reminiscent of temperature or humidity are inherently linked to the time of 12 months and hour of the day, as are components like faucet water utilization, metropolis air pollution ranges, and journey patterns. In sure eventualities, even the day of the week might affect the dataset’s variability.
Therefore, entrusting this seasonal knowledge to our neural community might show helpful. At instances, this necessitates transitioning from a univariate enter to a multivariate strategy.
How will our neural community grasp this seasonality?
For the sake of illustration, let’s make the most of a dataset spanning two years (2022–2023) comprising hourly climate knowledge sourced from the official climate service web site of my city. I’ve meticulously compiled, crammed in lacking knowledge, and cleaned the dataset. You possibly can obtain it from here.
Whereas numerical knowledge is typical for goal variables in datasets, time knowledge requires preprocessing earlier than our neural community can derive significant insights from it.
Take into account the next instance: the timestamps 2023–12–31 23:00:00 and 2024–01–01 01:00:00. Being each solely two hours aside, in a dataset spanning a number of years their significance ought to be practically equal; therefore, their “values” ought to exhibit minimal disparity. Equally, this holds true for the hours 23:59 and 00:01 of consecutive days.
Let the transformation start
To rework our time knowledge right into a significant and steady set of values, devoid of interruptions between days, months, and years, we flip to trigonometry. Its equations encapsulate the essence of periodicity, repetitiveness, and steady variations — qualities intrinsic to the passage of time, from hours and days to months, seasons, and years.
By leveraging trigonometric features, particularly the cosine perform, we are able to seamlessly encode time right into a format that’s each interpretable and conducive to evaluation. This transformation allows us to characterize time as a steady, clean curve, facilitating a deeper understanding of temporal patterns and developments.
Right here’s how we implement this in Python:
import pandas as pd
import numpy as np
import math
import matplotlib.pyplot as plt#load the dataset
url = 'temperature_2y.csv'
df = pd.read_csv(url)
#convert column string date to sort datetime
df['dt'] = pd.to_datetime(df['dt'])
#get day of 12 months from date
df['dy'] = df['dt'].dt.day_of_year
#to radians >> 1 yr = 1 cycle
df["dyr"] = 2 * math.pi * df["dy"] / 365
#cosine of the day of 12 months
df["dyc"] = np.cos(df["dyr"])
#outcomes to vary 0..1
df["dyc"] = (df["dyc"] + 1) / 2.0
#plot
plt.plot(df['dt'], df['dyc'])
plt.present()
With this dataset we use one year per 12 months. With a dataset spanning a number of years together with leap years, it’s possible you’ll select a extra precise variety of days in a 12 months: 365.25
Plot the column [dyc]:
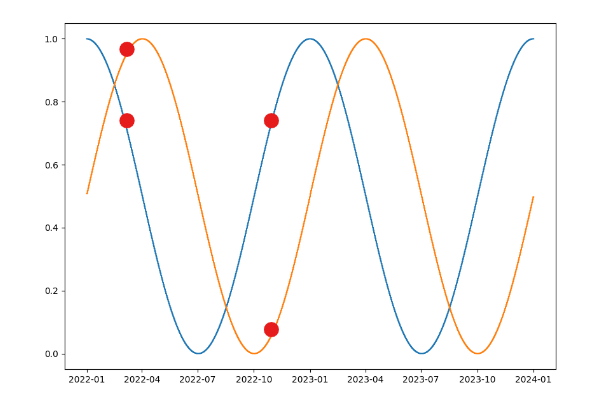
We will now see the info forming a significant, steady set of values through the years, following a repeating sample the place the y-values stay constant for a similar interval of the 12 months in annually (depicted by the blue dots added manually to the graph). This illustrates the idea of seasons.
But there stays a difficulty to deal with. Upon analyzing the plot, we discover that for every particular person 12 months, there are at all times two dates sharing the identical y-value (indicated by the crimson dots). This may be perplexing, because it implies {that a} day in February holds the identical worth as a day in November.
Trigonometry as soon as once more involves our help, providing an answer via the sine perform.
#sine
df["dys"] = np.sin(df["dyr"])
#vary 0-1
df["dys"] = (df["dys"] + 1) / 2.0#plot
plt.plot(df['dt'], df['dyc'])
plt.plot(df['dt'], df['dys'])
plt.present()
Now, our dataset consists of two columns, [dyc] and [dys], representing the second of the 12 months. Any day with the identical cosine worth as one other day inside a given 12 months could have a distinct sine worth. Now each values for a day uniquely establish a particular day of the 12 months.
You possibly can experiment with the hour part of a day from the identical dataset. Moreover, exploration can prolong to the day of the week. It’s vital to notice that the day of the week holds no correlation with climate; whether or not it’s Sunday or Monday will not be associated to wheather.
Furthermore, attempt to embrace wind route and velocity, transformed as effectively. It’s additionally doable to combine the wind velocity worth into the cosine and sine values, enhancing the illustration of temporal and meteorological patterns throughout the dataset.
Conclusion
Trigonometry equips us with the means to rework seemingly unwieldy knowledge right into a precious asset.
By incorporating seasonality knowledge right into a sequential dataset for neural community coaching, we are able to doubtlessly improve prediction accuracy.
Nevertheless, it’s essential to discern whether or not the seasonality knowledge derived from the dataset’s unique timestamp holds significance for the goal knowledge sequence. As an example, utilization of irrigation water might correlate with the time of 12 months, whereas the closing worth of a NASDAQ quote usually might not. Due to this fact, make considered consideration when deciding if temporal options could also be included in your dataset for coaching.